信息熵的引入是为了解决字符编码问题。 给定一篇文章,它由一些字符组成,每个字符有相应的出现次数,如何给每个字符赋予一个二进制编码,使得编码后的文章长度最短? 注意,这里的编码需要保证一个字符不是另一个字符的前缀,比如一个字符的编码如果是01,那么其余的字符编码不能是0,也不能以01开头。这意味着什么?如果把所有二进制串组成的集合称为编码空间,那么显然01这个编码就占了整个编码空间的四分之一!下图展示了原因:
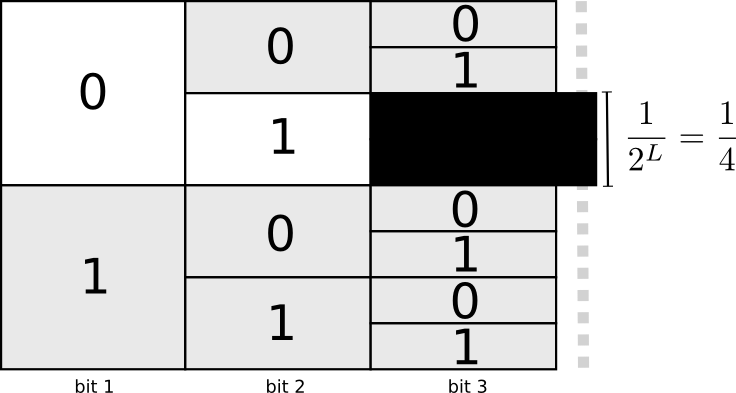
很容易把这个结论推广:一个长度为$L$的编码占据了整个编码空间的$2^{-L}$。 一个字符的编码越短,占的编码空间越多。回到问题本身,如果字符数量很多,意味着每个字符的编码都不能占太多编码空间,意味着每个字符的编码需要比较长才行。但我们又希望总的长度比较小,怎么使长度最小呢?直观来说,出现多的字符编码应该短一点,出现少的字符编码可以长一些。记一共有 $n$ 的字符,每个字符的出现频率是 $p_1,\cdots,p_n$,每个字符的编码长度为 $l_1,\cdots,l_n$。如果编码是合法的,那么有 $\sum_{i=1}^n2^{-l_i}≤1$。 可以证明,如果每个字符占据的编码空间刚好等于自身出现的频率时,平均编码长度最短。 也就是说,当 $p_i=2^{-l_i}$时,即 $l_i=-\log_2 p_i$时,$\sum_{i=1}p_il_i$最小。这其实是证明一个不等式:
\[\sum_{i=1}^n p_il_i\ge \sum_{i=1}^n -p_i\log_2 p_i\]证明如下:
\[\begin{aligned} \sum_{i=1}^n p_i(l_i+\log p_i) &=\sum_{i=1}^n p_i\log (2^{l_i}p_i)\\ &=-\sum_{i=1}^n p_i\log (\frac{2^{-l_i}}{p_i})\\ &\ge -\log(\sum_{i=1}^n p_i\frac{2^{-l_i}}{p_i})\\ &=-\log(\sum_{i=1}^n 2^{-l_i})\\ &\ge -\log 1 = 0 \end{aligned}\]第一个不等式是因为Jensen不等式,第二个是因为合法的编码需要满足 $\sum_{i=1}^n2^{-l_i}≤1$。
不等式的右边只和字符的分布有关,即最短编码完全取决于字符的概率分布,给这个最短的平均编码长度起一个名字信息熵,记为 $H(X)=E_{x\sim p}[-\log_2 p(x)]$,或者定义为 $H(X)=E_{x\sim p}[-\ln p(x)]$。在类别分布下,熵表示平均编码长度,如果编码出现越没有规律,即越“随机”,每个字符就要用更长的编码进行描述,熵也就越大。这个定义对于连续的概率分布也可以计算,但是此时他就不表示最短平均编码长度了,因为概率密度函数 $p(x)$ 可能大于0,导致 $-\ln p(x)$为负,无法表示长度。这时候,熵只能衡量随机变量有多“随机”。
交叉熵
\[H(p,q)=E_{x\sim p}[-\ln q(x)]=D_{KL}(p\|q)+H(p)\]就是用 $q$ 分布的编码在 $p$ 分布上的长度,如果 $p=q$,那么这个长度是最短的,就是 $H(p)$;如果$p\ne q$,那么$H(p,q)$相较于最短编码长度 $H(p)$ 会多出来 \(D_{KL}(p\| q)\) 这么多,定义它为KL散度,衡量了两个分布之间的差异。
KL散度
KL散度用来衡量两个分布之间的差异:
\[D_{KL}(p\|q)=H(p,q)-H(p)=E_{x\sim p}[-\ln \frac{q(x)}{p(x)}]\]-
根据定义可以看出,如果希望KL散度小,$p(x)$ 比较大的时候 $q(x)$ 也要大;$p(x)$小的时候,$q(x)$可大可小
-
可以证明KL散度的取值范围是$[0,\infty)$,两个分布的KL散度为0当且仅当两个分布相等
-
注意 \(D_{KL}(q\|p)\ne D_{KL}(p\|q)\),因此KL散度不是一个距离度量
-
通常会把目标分布放在前面,即 \(D_{KL}(p\|q)\) 中的 $p$ 是目标分布
比如$p$是狄拉克分布(one-hot向量),这要求$q(x)$在相应的也很大。
-
类别分布的KL散度最大值是 $\ln N$,$N$是类别个数
-
KL散度可能取到无穷大(无意义),这会实践中会导致一些问题