Markov Decision Process(MDP)是一个四元组 $<S,A,P,R>$：
-
$S$ 是状态集合：在$t$时刻的状态记为 $S_t$
-
$A$ 是行为集合：在$t$时刻的行为记为 $A_t$，有时候行为集合与状态有关，记为 $A(s)$
-
$P$ 是状态转移概率分布：$P(S_{t+1}=s’|S_t=s,A_t=a)$，表示在状态 $s$ 下选择行为 $a$ 后，转移到 $s’$ 的概率，简记为 $P(s’|s,a)$
-
$R$ 是奖励函数：$R:S\times A\times S→\mathbb{R}$，记 $R(s,a,s’)$ 为在状态 $s$ 下选择行为$a$到达状态 $s’$ 的奖励。在 $t$ 时刻的奖励用 $r_t$ 表示
策略
策略是智能体在状态 $s$ 下选择行为$a$的概率，记为 $\pi(a|s)$。如果是确定性的策略，则用 $a=\pi(s)$表示。
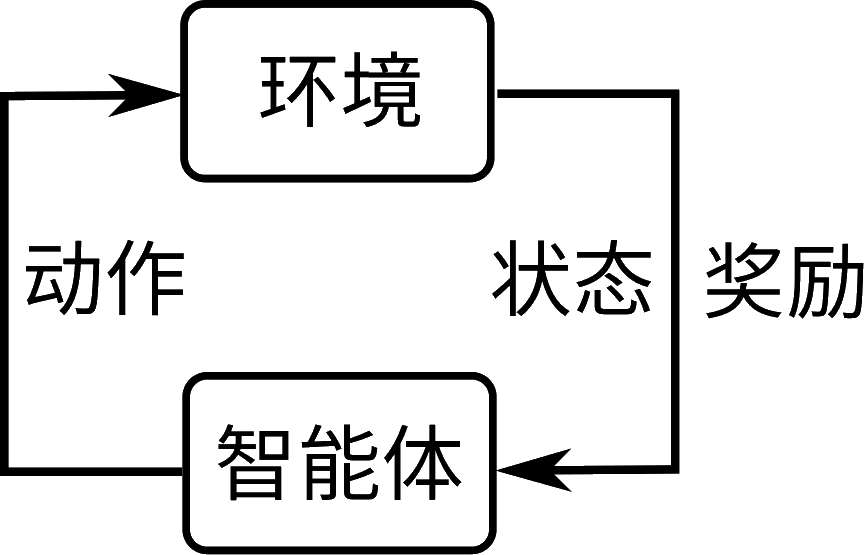
如上图所示，与监督学习从数据中学习不同，强化学习通过与环境交互获得反馈进行学习，而MDP用数学建模了这个与环境交互的过程。具体来说，Agent处在一个状态 $s$，根据自己的策略 $\pi$ 做出行为 $a$ 后，就会得到环境反馈的奖励 $r$，并根据状态转移概率分布 $P$ 到达新的状态 $s’$。强化学习是学习一个让长期奖励最大化的策略
值函数
强化学习的目标是最大化长期的奖励，因此我们需要定义一个能代表长期奖励的量进行优化，通常采用的是回报（return），定义为：
\[G_t=r_{t+1}+\gamma r_{t+2}+\cdots\]$\gamma\in[0, 1]$ 称为 折扣因子，如果 $\gamma$ 更接近1，表示 $G_t$ 更关注长期利益，反之更短视。通常 $\gamma$ 取0.9，0.99之类的值。
在强化学习中，目前有两大类学习策略的方法：
-
一种是直接学习一个函数作为策略，叫策略梯度法，使用神经网络表示策略 $\pi_{\theta}(\cdot|s)$，然后用梯度下降来训练神经网络，这种方比较直接，但是很多其中涉及到的很多思想来源于下面的方法，因此这个后面再说。
-
一种是间接的学习策略，是基于值函数的方法，具体来说是定义两个函数：
- 状态值函数：$V^{\pi}(s)=E[G_t|S_t=s]$，表示从状态 $s$ 开始，回报的期望，也叫V函数
- 行为值函数：$Q^{\pi}(s,a)=E[G_t|S_t=s,A_t=a]$，表示在状态 $s$ 做出行为 $a$ 后，回报的期望，也叫Q函数
注意值函数是依赖于策略的，上标为 $\pi$ 表示在策略 $\pi$ 下的值函数。有了Q函数之后可以通过求解 $\text{argmax}_a Q(s,a)$ 来获取行为，也就得到了一个基于Q的策略。
基于值函数的方法是基础，所以先介绍后者。
值函数性质
对于给定的策略，两个值函数的关系为（省略了上标 $\pi$）：
\[\begin{aligned} V(s) =& E_{a\sim \pi(\cdot|s)}[Q(s,a)] \\ Q(s,a) =& E_{s'\sim p(\cdot|s,a)}[R(s,a,s')+\gamma V(s')] \end{aligned}\]这样就得到了一个方程。在给定策略的情况下，如果状态空间和动作空间都是离散的，我们可以根据这个方程解出 V 和 Q。定义 $P^{\pi}(\cdot|s)=\int_a P(\cdot|s,a)\pi(a|s)$，表示给定策略下的状态转移分布。离散情况下，V函数是个向量，Q函数是矩阵，$P^{\pi}$ 也是个矩阵，就可以得到矩阵形式的方程：
\[\begin{aligned} v &= P^{\pi}Q = r + \gamma P^{\pi}v \\ Q &= P^{\pi}[r + \gamma v] \end{aligned}\]给定一个策略，可以通过求解第一个式子得到V函数，然后用第二个式子求出Q函数。第一个式子怎么求呢？理论上可以用矩阵求逆的方法去求，但实践中更多迭代的算法。第一个式子可以看成 $v=T^{\pi}(v)$，这里 $T^{\pi}$ 函数叫贝尔曼算子。解这个方程其实是求解不动点，在 $T^{\pi}$ 满足一定条件的情况下，使用不动点迭代，任意初始化 $v$ 都可以收敛于 $v^{\pi}$，具体算法后面会介绍。
最优值函数与最优策略
-
最优值函数：
- 最优状态值函数：$V^*(s)=\max_{\pi}V^{\pi}(s)$
- 最优行为值函数：$Q^*(s)=\max_{\pi}Q^{\pi}(s,a)$
这里的最优是在所有状态下最优，也就是帕累托最优。一个反直觉的地方是，两个策略可能一个在这个状态更好，一个在那个状态更好，而不存在在所有状态都更好的价值函数。但实际上因为这个过程是马尔可夫的，可以把每个状态看成独立的，每个状态上都有最好的策略。
-
定义偏序关系 $\pi≥\pi’$ 为 $\forall s\in S(V^{\pi}(s)≥V^{\pi’}(s))$
根据前面 V 和 Q 的关系，容易得到如果 $\pi≥\pi’$，也有 $\forall s\in S,\forall a\in A(Q^{\pi}(s,a)≥Q^{\pi’}(s,a))$。注意这里是采取相同的 $a$ 的情况下。反过来也正确。
定理：对任意的MDP，以下性质成立：
-
$\exists\pi_*\forall\pi(\pi_*\ge\pi)$，这说明最优策略总是存在（但不一定唯一）
-
$V^*(s)=V^{\pi_*}(s)$，最优策略的V函数就是最优V函数。给定最优策略，$V^{\pi^*}(s)$在所有状态都是最优的。
-
$Q^*(s,a)=Q^{\pi_*}(s,a)$，最优策略的Q函数就是最优Q函数。
最优策略可能不唯一，但是最优值函数唯一，求解值函数的目标就是找到这个最优值函数，进而得到一个最优策略。
定理：若$\forall s\in S$，取$\pi’(s)=\text{argmax}_a Q^{\pi}(s,a)$，则$\pi’≥\pi$，并且等号成立当且仅当$Q^{\pi}=Q^*$
这个定理的含义很简单，对任意的状态$s$，如果存在2个行为 $a,a’$ 使得 $Q(s,a)$ 和 $Q(s,a’)$ 不一样，那么总是可以选择 \(\text{argmax}_a Q(s,a)\) 使得 $Q(s)$ 变大。这样我们就得到了一个改进策略的方式，不断通过对Q函数取argmax得到更好的策略，再根据更好的策略求解它的Q函数，继续根据Q函数得到更好的策略，重复这个过程，最后得到一个最优的Q函数。
这个定理成立简单理解是因为 $ V(s)=E_{ a \sim \pi(\cdot | s)}[Q(s,a)] \le \max_a Q(s,a) $，这说明对任意的状态 $s$，V函数都得到了改进，根据前面偏序关系的定义就可以推出 $\pi’\le\pi$。
定理：$\pi(s)=\text{argmax}_a Q^*(s,a)$是最优策略。
对任意的策略$\pi’$，由于$Q^*(s,a)≥Q^{\pi’}(s,a)$，所以$\pi≥\pi’$，所以$\pi$是最优策略。
综合上面2个定理，我们得到了一个算法思路：根据Q函数改进策略，根据改进的策略得到新的Q函数，重复这个过程得到最优Q函数，进而得到最优策略，这是后面要介绍的策略迭代算法。
Bellman方程
根据前面V函数和Q函数的关系：
\[\begin{aligned} V(s) =&E_{a\sim \pi(\cdot|s)}[Q(s,a)] \\ Q(s,a) =& E_{s'\sim p(\cdot|s,a)}[R(s,a,s')+\gamma V(s')] \end{aligned}\]容易得到：
\[\begin{aligned} V(s)&= E_{a\sim \pi(\cdot|s)}[E_{s'\sim P(\cdot|s,a)}[R(s,a,s')+\gamma V(s')]] \\ Q(s,a)&= E_{s'\sim p(\cdot|s,a)}[E_{a'\sim \pi(\cdot|s')}[R(s,a,s')+\gamma Q(s',a')]] \end{aligned}\]这个叫Bellman方程（两个方程都是），如果已知策略，可以利用该方程求解 $V$ 和 $Q$。注意Bellman方程是针对一个策略而言的，用来求解这个策略的V函数和Q函数。
策略迭代
策略迭代是求解Bellman方程的算法，要求状态空间和动作空间是有限的，算法流程是：
-
初始化 $V(s)=0$，初始化策略 $\pi(a|s)=\frac{1}{|A(s)|}$
-
迭代$N$次：
-
策略估计，就是求$V_{\pi}$，重复计算以下公式即可：
\[V(s)\leftarrow E_{a\sim \pi(\cdot|s)}[E_{s'\sim P(\cdot|s,a)}[R(s,a,s')+\gamma V(s')]]\]一个直观的理解是，$V(s)$ 初始为0，迭代一次就是计算了 $E[r_{t+1}|S_t=s]$，两次则是 $E[r_{t+1}+\gamma r_{t+2}|S_t=s]$，计算无穷次就是 $E[G_t|S_t=s]$ 了。这是动态规划角度的理解，也可以从不动点迭代的角度理解，就是不断的计算 $T$ 函数进行迭代。不过这个算法不重要，也不需要详细理解。 -
策略改进，根据前面的定理改进策略
\[\begin{aligned} Q(s,a)\leftarrow &E_{s'\sim P(\cdot|s,a)}[R(s,a)+\gamma V(s')] \\ \pi(s) \leftarrow &\text{argmax}_{a}Q(s,a) \end{aligned}\]前面证明了这样可以得到一个更好的策略，直到得到最优策略才不会变得更好，不过实践中迭代$N$次得到一个比较好的策略就行。
-
不一定要求$V$，求$Q$也行，哪个方便求哪个。
Bellman最优性方程
前面介绍了Bellman方程和策略迭代算法，这个算法的缺点是速度比较慢，需要先迭代很多次进行策略估计，再改进策略，这个过程又要重复很多次。一个更好的思路是，如果直接求解最优策略的Bellman方程，是不是可以直接解出最优值函数？
如果有 $Q^*$ 以及最优策略 $\pi^*(s)=\text{argmax}_a Q^*(s,a)$，可以得到 $V^*(s)=\max_a Q^*(s,a)$，于是Bellman方程变为以下形式：
\[V^*(s) = \max_a E_{s'\sim P(\cdot|s,a)}[R(s,a,s')+\gamma V^*(s')] \\ Q^*(s,a)= E_{s'\sim P(\cdot|s,a)}[ R(s,a,s')+\gamma \max_a Q^*(s',a) ]\]该方程称为Bellman最优性方程，也可以写成 $v=T^*(v)$。直接用不动点迭代解这个方程就能得到比策略迭代更好的值迭代算法。
值迭代
值迭代是求解Bellman最优性方程的算法，比策略迭代收敛更快（有时候），算法流程是：
-
$V(s)=0$
-
迭代$N$次：
\[V(s)\leftarrow \max_aE_{s'\sim P(\cdot|s,a)}[R(s,a,s')+\gamma V(s')]\] -
$Q(s,a)\leftarrow E_{s’\sim P(\cdot|s,a)}[R(s,a,s’)+\gamma V(s’)]$
-
$\pi(s)\leftarrow \text{argmax}_aQ(s,a)$
可以看出值迭代比策略迭代简单，照着一个公式迭代就行，后面两步只是把V函数转换为Q函数，进而得到策略 $\pi$。
理解值迭代
-
策略迭代收敛慢是因为需要迭代很多次进行策略评估，实际上如果策略评估只迭代一次就是值迭代，证明如下：
如果策略估计只迭代一次，那么策略迭代的每次迭代就是进行以下三步（给它加上角标 $t$）： $$ \begin{aligned} V_{t+1}(s)\leftarrow & E_{a\sim \pi_t(\cdot|s)}[E_{s'\sim P(\cdot|s,a)}[R(s,a,s')+\gamma V_t(s')]] \\ Q_{t+1}(s,a)\leftarrow & E_{s'\sim P(\cdot|s,a)}[R(s,a,s')+\gamma V_{t+1}(s')] \\ \pi_{t+1}(s)\leftarrow & \text{argmax}_{a}Q_{t+1}(s,a) \end{aligned} $$ 这三行合并成一个就是值迭代了。把第二行带入第一行可以得到，$V_{t+1}(s)\leftarrow E_{a\sim\pi_t(\cdot\|s)}[Q_t(s,a)]$。进一步用第三行 $$\pi_{t}(s)\leftarrow \text{argmax}_{a}Q_{t}(s,a)$$ 去掉期望： $$ \begin{aligned} V_{t+1}(s)\leftarrow E_{a\sim\pi_t(\cdot|s)}[Q_t(s,a)] =& \max_a Q_{t}(s,a)\\ =& \max_a E_{s'\sim P(\cdot|s,a)}[R(s,a,s')+\gamma V_t(s')] \end{aligned} $$ 这样就推出来了值迭代。
-
值迭代就是动态规划，可以用来求图上的最短路之类的（Viterbi算法）。因为离散的MDP其实也是个图，只是状态转移是概率性的，而Viterbi这种算法的动态规划是有向无环图（DAG）上的，而且是确定性的，不需要像值迭代一样在整个图上迭代多次，也不需要求期望。