lurenjie's Blog

【强化学习】Model-Free算法

 
  • 2025年 09月26日

马尔可夫决策过程是四元组 $<S,A,P,R>$，上一篇文章介绍的值迭代算法依赖于 $P$ 和 $R$ 去求解最优策略。但是，实际应用中我们并不知道具体的 $P$ 和 $R$。那我们知道什么呢？我们能获取的是和环境交互来获取reward以及新的状态，如下面的代码展示的：

done = False
state = env.reset()
while not done:
    action = agent.take_step(state)
    state_, reward, done = env.step(action)
    agent.update(state, action, state_, reward, done)  # 这里使用强化学习算法
    state = state_

为此，需要新的算法在这种情况下学习最优策略，也就是所谓的Model Free的方法。有一点需要注意的是，前面我们通过值迭代求解 V 函数，然后根据 V 函数结合状态转移函数 $P$ 计算 Q函数，最后得到策略。而在不知道 $P$ 的情况下，我们没法由 $V$ 计算得到 $Q$，因此必须直接求解 $Q$（当然后面也有算法需要用到 $V$）。

蒙特卡洛法

蒙特卡洛法通过采样的方式估计Q函数，可以放在策略迭代算法中的策略估计这一步。

首先介绍轨迹的概念，它指依照一定策略，从起始状态开始到终止状态经历的状态、动作、奖励的序列，通常记为 $\tau$。比如$\tau=<s_0,a_0,r_1, s_1,s_1,a_1,r_2,…, s_{T-1},a_{T-1},r_T,s_T>$，注意这里要求存在终止状态，比如游戏、围棋之类的要能够结束。有一些场景可能不存在终止状态，导致蒙特卡洛法无法使用，不过蒙特卡洛法本身也只是一个引子，实际不用这个，无需在意。

有了轨迹之后，我们就可以给轨迹里面的每个 $<s_t, a_t>$ 统计它的return，也就是 $G_{s_t,a_t}=\sum_{i=0} \gamma^i r_{t+i}$。蒙特卡洛方法是用平均值近似期望值，即 $Q(s,a)\approx \frac1N\sum_{i=1}^N G_{s,a}$，在这里就是求出很多轨迹的回报，然后取平均来估计价值函数（并且使用顺序估计求平均）：

  • 初始化 $Q(s,a)=0$，$\pi(s,a)=1/|A(s)|$，$n(s,a)=0$

  • 迭代 $N$ 次：

    • 用策略 $\pi$ 跟环境交互，得到一条轨迹 $\tau=<s_0,a_0,r_1, s_1,s_1,a_1,r_2,…, s_{T-1},a_{T-1},r_T,s_T>$
    • $G\leftarrow 0$
    • 遍历 $t = T-1,T-2, \cdots,0$
      • $G\leftarrow \gamma G+r_{t+1}$
        倒着遍历求return是一个常见的trick
      • $s\leftarrow s_t, a\leftarrow a_t$
        去掉角标 $t$ 主要是为了后面少打公式。
      • $n(s,a)\leftarrow n(s,a)+1$
        计数，用来取平均
      • $Q(s,a)←Q(s,a)-\frac1{n(s,a)}[Q(s,a)-G]$
        因为 $N$ 个数的平均数$\bar x_N$ 可以写成迭代的形式 $ \bar x_N= (1-\frac1N)\bar x_{N-1}+\frac{1}{N} x_N = \bar x_{N-1} - \frac1N (\bar x_{N-1} - x_N) $，这个看起来像是梯度下降算法一样（$\frac1N$ 对应学习率，$\bar x_{N-1} - x_N$ 对应梯度），比较好记，实际上也的确和梯度下降算法高度相关，具体可以参考后面的随机近似。
        公式也可以改为：$Q(s,a)←Q(s,a)-\alpha[Q(s,a)-G]$，其中 $\alpha$ 是学习率，原理也是参考后面的随机近似部分。

整体来看，蒙特卡洛法就是用均值去估计Q函数，只不过因为Q是个函数，在很多 $<s,a>$ 上都有值，所以每个函数值都要用均值去估计。该算法的一个细节是充分利用整个轨迹，把轨迹上的 $<s,a>$ 全部都用来更新Q函数。

同策略与异策略

在Model Free的算法中，需要探索环境以获取轨迹 $\tau$，由于我们希望学习到的策略是确定性的，但为了探索环境又需要随机性的策略来见到各种 $<s,a>$，为此可以维护两个策略，一个用来获取 $\tau$，一个是我们期望学到的策略，这引申出2类算法：

  • 同策略（On-policy）：探索环境与学习的策略是同一个策略（根据自己的经验学习）
  • 异策略（Off-policy）：探索环境与学习的策略不是同一个策略（看别人的经验学习，用别的策略方式收集一堆数据然后训练自己的策略）

我们希望得到的策略是确定性策略 $\text{argmax}_a Q(s,a)$，给它引入随机性的常见的办法是 $\epsilon$-greedy:

\[\pi(a|s)=\begin{cases} \frac{\epsilon}{|A(s)|} + 1 - \epsilon & a=\text{argmax}_a Q(s,a)\\ \frac{\epsilon}{|A(s)|} & a\ne\text{argmax}_a Q(s,a) \end{cases}\]

类似于分类里面的label smoothing分摊一些概率到其它类别里面，这里则是分摊到其它action。

同策略蒙特卡洛强化学习算法

这里给出一个完整的基于蒙特卡洛的强化学习算法，利用蒙特卡洛估计替代策略迭代算法的策略估计部分：

  1. 初始化 $Q(s,a)=0$，$n(s,a)=0$，$\pi(a|s)=1/|A(s)|$

  2. 迭代 $N$ 次：
    • 策略估计
      • 根据策略 $\pi$ 得到一条轨迹$\tau=<s_0,a_0,r_1, s_1,s_1,a_1,r_2,…, s_{T-1},a_{T-1},r_T,s_T>$
      • $G\leftarrow 0$
      • 遍历 $t = T-1,T-2, \cdots,0$
        • $G\leftarrow \gamma G+r_{t+1}$
        • $s\leftarrow s_t, a\leftarrow a_t$
        • $n(s,a)\leftarrow n(s,a)+1$
        • $Q(s,a)←Q(s,a)+\frac1{n(s,a)}[G-Q(s,a)]$

    • 策略改进

      \[\pi(a|s)=\begin{cases} \frac{\epsilon}{|A(s)|} + 1 - \epsilon & a=\text{argmax}_a Q(s,a)\\ \frac{\epsilon}{|A(s)|} & a\ne\text{argmax}_a Q(s,a) \end{cases}\]
  3. 得到最终策略：$\pi(a|s)=\text{argmax}_a Q(s,a)$

注意这里只用一条轨迹更新完Q函数后，直接就进行策略改进了，原因是值迭代证明了策略估计部分只要更新一次就足够好了。蒙特卡洛法估计Q函数的效率比较低（估计量的方差比较大），与之对应的算法是时间差分，需要一些随机近似的数学基础才能理解，所以下面先介绍随机近似。

随机近似

随机近似是一类近似算法，这里介绍随机近似里的零点估计问题。求严格单调函数 $f(\theta)$ 的零点可以用数值计算里的方法来求，比如不动点迭代。但如果 $f(\theta)$ 是得不到的，只能获得带噪声的数据 $z(\theta,\epsilon)$，这里$\epsilon$表示随机噪声，$z(\theta,\epsilon)$ 表示受噪声影响，噪声满足：

\[f(\theta)=E_{\epsilon}[z(\theta,\epsilon)]\]

这表明 $z$ 其实就是带噪声的 $f$，意思是我们只能获取 $f(\theta)$ 带噪声的函数值，无法获取准确值。这种情况下怎么求零点？这是Robbins-Monron算法要解决的问题。

在介绍RM算法之前，先说明一下这个求零点的问题在机器学习中还挺常见，比如：

  • 如果 $\theta$ 是自变量，$f(\theta)$ 是某个函数的梯度，那么该问题就是一个优化问题，找到梯度为0的点（求极值）。
    此时 $z(\theta,\epsilon)$ 是mini-batch的梯度，因为batch上的梯度相较于完整梯度是有噪声的，这是随机梯度下降的场景。
  • 如果要估计 $X$ 的期望，令 $f(\theta)=\theta-E[X]$ 即可。在强化学习中我们要用均值估计Q函数，就可以用RM算法。

Robbins-Monro算法

记 $\theta^*$ 满足 $f(\theta^*)=0$，Robbins-Monro算法通过以下公式对 $\theta$ 进行迭代进行求解：

\[\theta_{t+1}\leftarrow \theta_t-\alpha_tz_t\]

其中 $z_t=z(\theta_t,\epsilon)$。这个算法是说，从 $\theta_0$ 开始迭代，在函数的 $\theta_t$ 处得到带噪声的函数值 $z_t$，然后用该公式迭代就能让 $\theta$ 收敛于零点 $\theta^*$。

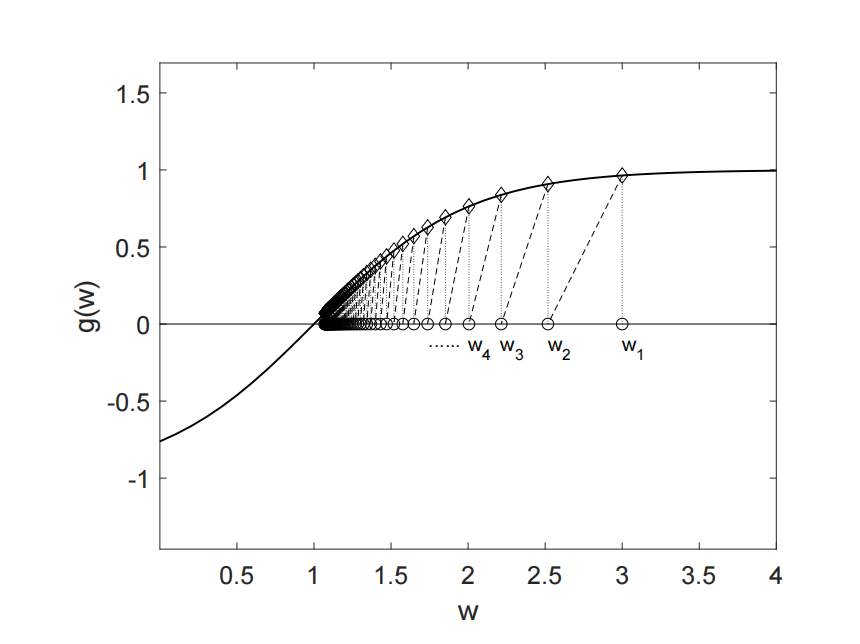
怎么理解这个算法呢？如上图所示（图中的 $w$ 对应这里的 $\theta$），如果 $z>0$，由于 $f$ 单调递增，就该让 $\theta$ 减去 $z$ 变小一点才能使 $f(\theta)$ 接近0；如果 $z<0$，就该减去 $z$ 让 $\theta$ 大一点。总之就是减 $z$，前面再乘以学习率控制调整的幅度。

RM算法只有在一定条件下能依概率收敛到零点，下面是需要满足的条件：

  • $f(\theta)$ 严格单调递增，且导数不能为正无穷
  • $z(\theta,\epsilon)$ 有界
    就是噪声不能离谱
  • $\alpha_t$需要满足： \(\sum\limits_{t=1}^{\infty}\alpha_t = \infty, \sum\limits_{t=1}^{\infty}\alpha^2_t = 0 \notag\)
    学习率的一阶和无穷大，保证了步长不要收敛太快；二阶和有限，保证了步长足够小，最终收敛。

一般学习率设为常量是很常见的，虽然常量学习率不满足上面的条件，但是设置一个比较小的学习率最后能在收敛的地方震荡，也能达到不错的结果，所以无需担心，各种学习率的scheduler也能用。

RM算法估计均值

要估计均值，可以转换为零点估计问题，令 $f(\theta)=\theta-E[X]$ 即可，这显然是单调递增的，满足前面的条件。每次观测到一个$x_t$，那么$z_t=\theta_t-x_t$。套上RM算法的公式：

\[\theta_{t+1} \leftarrow \theta_t - \alpha_t(\theta_t - x_t)\]

可以看出这个和前面的蒙特卡洛估计的公式很类似，这就解释了前面为什么说可以把 $\frac1{n(s,a)}$ 换成固定的学习率。

时间差分算法

介绍了RM算法之后，就可以回到强化学习的场景介绍Time difference（TD）算法了，时间差分比蒙特卡洛收敛更快。

TD

考虑轨迹$<s, a, r, s’, a’,\cdots>$，时间差分使用$r+\gamma V(s’)$来近似回报 $G$，由于估计的过程中用到了 $V$ 自身，因此说TD是bootstrap的。TD的更新公式是：

\[V(s)\leftarrow V(s)-\alpha[V(s) - (r + \gamma V(s'))]\]

这里 $r+\gamma V(s’)$ 称为TD Target，$r+\gamma V(s’) - V(s)$称为TD Error，即期望的值与实际值的差异。这个公式其实就是前面RM算法估计均值的公式。

MC与TD的对比

时间差分（TD）和蒙特卡洛（MC）的直观的区别是什么？从公式上看，唯一的区别是一个用真实的 $G$，一个用 $r+\gamma V(s’)$。这个差异的具体效果可以从一个例子来理解（来源于distill博客）：

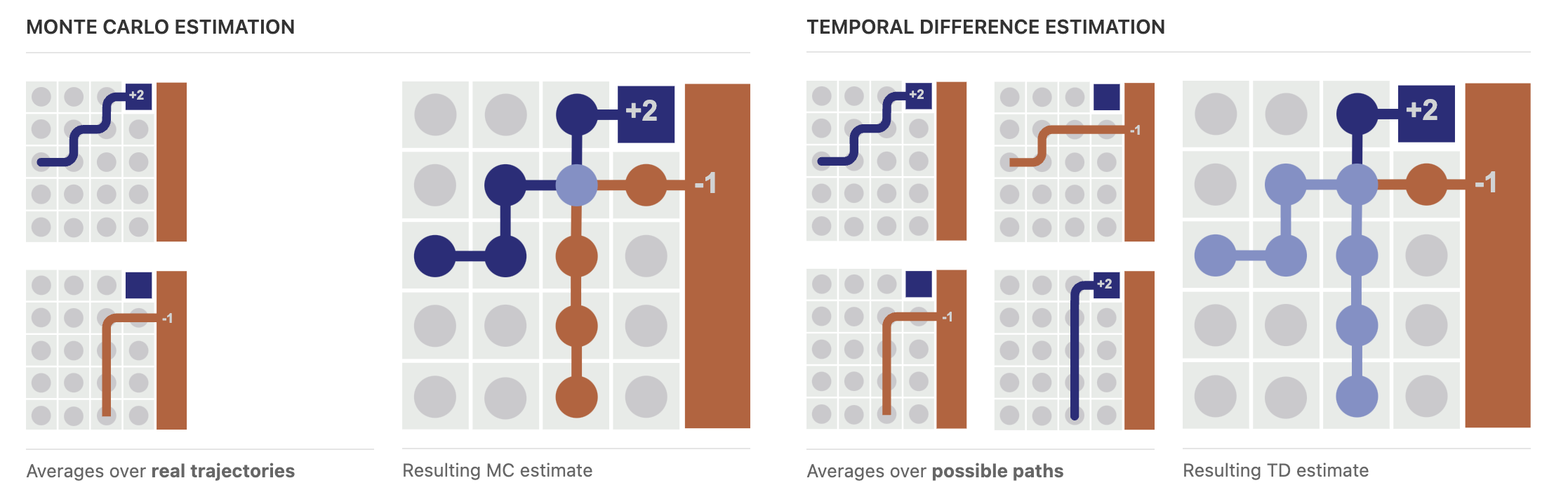
  • 上图左半部分是蒙特卡洛法，右半边是时间差分
  • 模型一开始走完了一条轨迹（深蓝色轨迹），更新轨迹上的V函数值，这个时候TD和MC没有区别
  • 在走第二条轨迹的时候（橙色轨迹）
    • 其中状态 $s’$ 和第一条轨迹重合了（上图所示的浅蓝色交叉点），那么在两条轨迹中 $s’$ 的前面状态 $s$ 的更新上，MC只考虑了走过的2条轨迹；而TD考虑了排列组合的所有情况，因为它用的是 $r+\gamma V(s’)$，而 $ V(s’)$ 已经用2条轨迹更新了，所以说TD更充分地利用了收集的轨迹。对应到图中就是时间差分的浅蓝色顶点更多，表明这些顶点上的值函数估计更准。

TD是每走一步就更新，MC是走完一条轨迹得到 $G$ 才更新，二者的折中是走n步来近似 $G$，也就得到了n步TD方法，叫TD(n)，用 $r_0 + \gamma r_1 + \cdots +\gamma^n r_n+\gamma^{n+1}V(s_{n+1})$ 近似 $G$。

最后对比一下TD和MC：

  • TD是每一步都能更新 $v$ 更灵活；MC必须经过一条轨迹才能更新，二者的折中是TD(n)
  • TD是高偏差低方差的（如果不倒着遍历轨迹，前期Q函数不准会带来偏差）；MC是无偏高方差的，TD(n)是二者的折中
  • TD不需要轨迹能终止；MC必须要求能终止

TD一般比MC收敛更快，而且更灵活，在强化学习中更常见，后续的算法全部基于TD。二者的折中TD(n)是更好的，近些年的深度学习算法则是TD(n)使用更多。

Model-Free算法

前面介绍了时间差分算法，这一部分介绍完整的基于时间差分的Model Free强化学习算法。

Sarsa

Sarsa算法流程如下：

  1. 初始化 $Q(s,a)=0$
  2. 迭代 $N$ 次：
    • 更新策略 $\pi$ 为 $\text{argmax}_a Q(s,a)$ 的 $\epsilon$-greedy策略
    • 在状态 $s$ 根据策略采取行为 $a$，获得奖励 $r$，到达状态 $s’$，然后再采取行为 $a’$
      这里依次出现了 $s,a,r,s',a'$，所以这个算法叫Sarsa。。。
    • $Q(s,a)\leftarrow Q(s,a)-\alpha[Q(s,a)-[\textcolor{red}{r+\gamma Q(s’,a’)}]]$
    • $s←s’$
  3. 得到策略 $\pi(s)\leftarrow \text{argmax}_a Q(s,a)$

Sarsa用了 $r+\gamma Q(s’,a’)$ 作为 $G$ 的估计（TD Target），正确的TD Target应该是 $r+\gamma V(s’)$，为什么Sarse这么做？注意到 $V(s’)$ 其实是 $Q(s’,a)$ 的期望，所以Sarsa是用随机变量代替了它的期望，这是一个方差比较大的估计，在策略稳定的情况下是ok的，需要策略满足GLIE条件（$\epsilon$ 要逐渐减小到0）才能收敛。

Expected Sarsa

Expected Sarsa算法是Sarsa算法的改进，流程如下：

  1. 初始化 $Q(s,a)=0$
  2. 迭代 $N$ 次：
    • 更新策略 $\pi$ 为 $\text{argmax}_a Q(s,a)$ 的 $\epsilon$-greedy策略
    • 在状态 $s$ 采取行为 $a$，获得奖励 $r$，到达状态 $s’$
    • $Q(s,a)\leftarrow Q(s,a)-\alpha[Q(s,a)-[\textcolor{red}{r+\gamma E_{a\sim \pi(\cdot|s’)}[Q(s’,a)]}]]$
    • $s←s’$
  3. 得到策略 $\pi(s)\leftarrow \text{argmax}_a Q(s,a)$

这显然是一个比Sarsa更合理的方案，和Sarsa的区别是它本质上在用RM算法估计下面的均值：

\[Q(s,a)=E_{s'\sim p(\cdot |s)}[r+\gamma V(s')]\]

Q-learning算法

最优策略的Q函数满足：

\[Q^*(s,a)=E_{s'\sim p(\cdot |s)}[r+\gamma\ \max_a Q(s',a)]\]

如果直接用RM算法估计这个均值可以得到迭代的公式是：

\[Q(s,a)\leftarrow Q(s,a)-\alpha[Q(s,a)-[r+\gamma \max\limits_aQ^\textcolor{red}{*}(s',a)]]\]

但是 $Q^\textcolor{red}{*}(s,a)$ 我们不知道，把它替换为 $Q(s,a)$ 就可以得到Q-Learning方法：

  1. 初始化$Q(s,a)=0$
  2. 迭代$N$次：
    • 更新 $\pi$ 为 $\text{argmax}_a Q(s,a)$ 的 $\epsilon$-greedy策略
    • 在状态 $s$ 根据策略 $\pi$ 采取行为 $a$，获得奖励 $r$，到达状态 $s’$
    • $Q(s,a)\leftarrow Q(s,a)-\alpha[Q(s,a)-[\textcolor{red}{r+\gamma \max\limits_aQ(s’,a)}]]$
    • $s\leftarrow s’$
  3. 得到策略$\pi(s)\leftarrow \text{argmax}_a Q(s,a)$

为什么这样做是合理的？其实正常的推导是考虑Bellman最优性方程，从求不动点的角度去证明Q-Learning的收敛性。不过这里我从RM算法的角度去说应该会直观一点，可以体现出Q-Learning想直接近似最优Q函数。实际上随着训练进行，$|Q(s,a)-Q^*(s, a)|$ 是不断减小的，这样也能解释上面的替换。如果每个状态访问无数次，Q-Learning算法的Q函数能依概率收敛于最优Q函数，但是实践中无法做到，Q-Learning有明显的bias。

Q-Learning算法是非常著名的算法，主要优点是它是Off-Policy的，更灵活。因为Q-Learning的希望近似的是最优Q函数而Sarsa希望近似的是当前策略的Q函数。相比之下Sarsa是On-policy的算法，因为它要用 $Q(s’, a’)$ 近似 $V(s’)$，如果换一个策略这个近似就不成立，要改成Off-policy的话需要使用重要性采样，比较麻烦。注意，虽然这里介绍算法的顺序是先介绍Sarsa、Expected Sarsa、Q-Learning，但实际上Q-Learning是最先提出的（1989年），Sarsa是后提出的（似乎是1994年？），最后才是Expected Sarsa。

Q-Learning虽然有Off-policy的优点，但是它的一个大问题是会高估（maximization bias），它是有偏估计，导致最终学到的策略比较激进。因为虽然我们是直接用RM算法估计Bellman最优性方程，但是我们没有获得随机变量的真实值，而是用bootstrap近似的，这个操作引入了偏差，导致后续的基于Q-Learning的深度强化学习算法DQN也存在高估问题。一种解决办法是使用Double Q-Learning算法，这个算法在深度学习时代也有用（DDQN）。

Double Q-Learning算法

Double Q-Learning维护两个Q函数 $Q_1$ 和 $Q_2$，并互相使用对方的值计算TD Target来更新自己：

  1. 初始化 $Q_1(s,a)=0，Q_2(s,a)=0$
  2. 迭代 $N$ 次：
    • 更新策略 $π$ 为基于 $Q_1(s,a)+Q_2(s,a)$ 的ϵ-greedy策略
    • 在状态 $s$ 根据策略 $π$ 采取行为 $a$，获得奖励 $r$，到达状态 $s’$

    • 以0.5的概率：

      \[\begin{aligned} a_∗ &← \text{argmax}_aQ_1(s',a) \\\ Q_1(s,a) &← Q_1(s,a)−α[Q_1(s,a)−[r+γQ_2(s',a_*)]] \end{aligned}\]

      否则：

      \[\begin{aligned} a_∗ &← \text{argmax}_aQ_2(s',a) \\ Q_2(s,a) &← Q_2(s,a)−α[Q_2(s,a)−[r+γQ_1(s',a_*)]] \end{aligned}\]
    • $s\leftarrow s’$
  3. 得到策略 $π(s)← \text{argmax}_a[Q_1(s,a)+Q_2(s,a)]$

这样做的好处是2个Q函数实际使用了不同的数据进行训练，用对方的Q函数取max不容易高估，因为两个函数一起高估的概率比较低（毕竟用的不同数据训练）。不过Double Q-Learning似乎也是有偏的？要直接近似最优值函数还是比较难的，只不过没有高估问题了。

总结

总结一下从策略迭代发展到Q-learnig涉及到的思想：

  • 直接求解Bellman最优性方程，这在值迭代和Q-Learning都有体现
  • 策略估计只迭代一次，在值迭代以及各种Model-Free算法中都有体现
  • 使用bootstrap的方式减小估计 $G$ 的方差，同时允许每一步都进行更新

最后，综合来看这些Model-Free算法，其实都是通过一定的策略去收集类似于 $<s, a, r, s’>$ 的数据对模型训练（这里就是Q函数）。在深度强化学习中，这些数据就是神经网络的训练数据，用来计算loss和反向传播，从这个角度理解其实深度强化学习比这里的内容更简单，只是相较于监督学习多了个自行收集数据的过程（叫rollout），而且深度强化学习完全没有理论证明。

搜索